3小時讀通幾何

序───3

第一章 幾何學入門
1-1 幾何是從哪裡來的？意義為何？
1-2 《幾何原本》的「點」、「線」、「面」
1-3 提高一個次元，解題立刻變簡單？
1-4 圓為什麼是360°？弧度又是什麼？
1-5 平行線竟然會相交…反思解題法！
1-6 簡化「內角和180°」的證明方法！
1-7 以轉鉛筆法測量角度
專欄：質疑歐幾里得？「幾何學中有帝王之路」的異想！

第二章 幾何的基礎在「變形」
2－1為什麼長方形面積是長×寬呢？
2－2面積不變，變成簡單的圖形
2－3改變形狀，簡化題目
2－4從三角形面積導出「數列公式」
2－5用面積思考鶴龜算，題目立刻變簡單
2－6食鹽水的濃度也能以面積法求出？
2－7蜂巢與狄利克雷圖
2－8三角形很堅固，四邊形比較弱
專欄：1796年3月30日發生的事情，解決了高斯對未來的煩惱

第三章 挑戰！不可思議的圓與π
3－1測量曲線的土地面積
3－2古埃及是用正方形來求圓面積？
3－3向萊因德紙草書的圓面積問題挑戰！
3－4用阿基米德窮盡法計算圓周率
3－5以直覺認識「圓的面積」
3－6 以重量求出圓周率的新方法！
3－7用牙籤求圓周率─布豐投針
3－8試證明圓周率比3.1大…
3－9內圓周和外圓周相差多少？
3－10克卜勒之從樸實的窮盡法發現了大世界！
專欄：阿基米德故意把錯誤的定理寫在信裡…

第四章 畢達哥拉斯定理與三角函數的智慧
4－1畢達哥拉斯定理是幾何學瑰寶！
4－2「無理數」誕生於幾何世界
4－3土地測量師與直角三角形
4－4頭腦體操：畢達哥拉斯定理的證明
4－5用三角形記憶sin、cos、tan
4－6運用廣泛的正弦定理、餘弦定理
4－7用木工角尺計算路徑
專欄：畢達哥拉斯「派」定理？

第五章 輕輕鬆鬆學會體積
5－1三角錐是角柱的1/3，實際體驗！
5－2卡瓦列里原理
5－3用卡瓦列里原理求出球體積！
5－4如何計算球的表面積
5－5推論地球的重量
5－6用圓頂平台求山的體積！
專欄：關孝和─將日本獨有的和算，提高至世界級

第六章 圓形的全等與相似
6－1全等與相似的誤解
6－2三角形的全等條件與相似條件
6－3利用相似測量金字塔高度
6－4以「空間圖形比」求出金字塔高度
6－5用棉紙測量樹的高度
6－6拋物線皆相似
6－7線對稱、點對稱
6－8徽章設計的對稱性問題
專欄：數學家泰勒斯的智慧

第七章 用積分求曲線面積
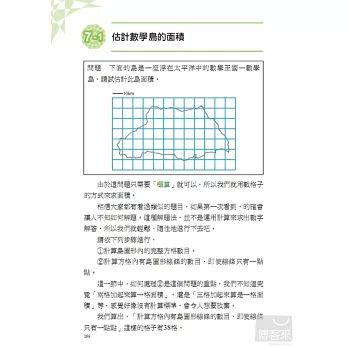
7－1估計數學島的面積
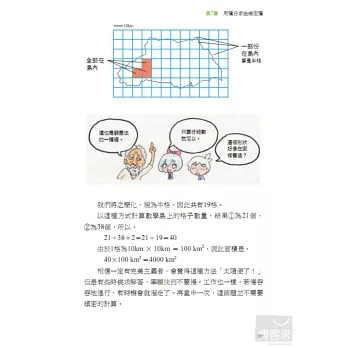
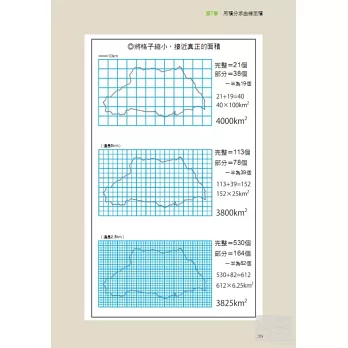
7－2數學島的真正面積
7－3曲線和直線所包圍的面積
7－4以積分算「區間」面積
7－5以積分計算Xn
7－6用切片來計算體積
7－7用積分求迴轉物體的體積
7－8證明圓錐體積「恰好是圓柱的1/3」
專欄：牛頓是「最後的蘇美人」？

第八章不可思議的「幾何宇宙」
8－1拓樸學是橡膠幾何學
8－2變形地圖是「切近本質」的拓樸學發想
8－3以「一筆畫發想」解開艱深問題
8－4「非歐幾里德」的新式幾何學
8－5拒絕菲爾茲獎與一百萬美元的數學家
8－6碎形為「自我相似」的幾何學
專欄：歐拉給公主的信－「幾何學中的帝王之路」
索引